数据结构入门——图

本文翻译自 Data Structures and Algorithms (DSA) 的系列文章有关图的章节，Google 翻译真好用。

在本篇文章中，我们将会探索非线性的数据结构——图，我们将会涉及到图的核心概念以及典型应用。

你可能现在就在使用那些用到了图和树这些数据结构的程序。比方说，你想要知道家和公司之间的最短距离，那么你就可以使用图算法来计算出答案。我们将会在后面探索这个以及一些其它有趣的挑战。

下面是我们将会在本文中介绍的一些操作：

	邻接表	邻接矩阵
Space	O(V + E)	O(V^2)
addVertex	O(1)	O(V^2)
removeVertex	O(V + E)	O(V^2)
addEdge	O(1)	O(1)
removeEdge (using Array)	O(E)	O(1)
removeEdge (using HashSet)	O(1)	O(1)
getAdjacents	O(E)	O(V)
isAdjacent (using Array)	O(E)	O(1)
isAdjacent (using HashSet)	O(1)	O(1)

基础知识

图是一种包含若干节点（node）的非线性数据结构，里面的节点可以有零个或者多个相邻的元素。我们称连接两个节点的线段为边（edge）。通常节点也被称作顶点（vertex）。

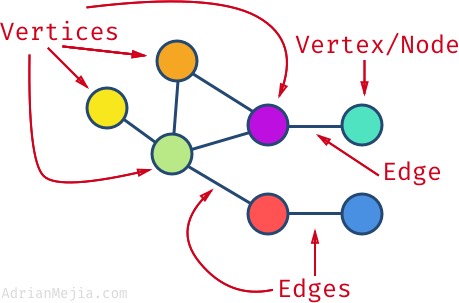
一个顶点所连接的边的数量被称为度（degree），例如，上图里的紫色顶点的度为 3，蓝色顶点的度为 1。

如果图里的边是双向的，那么这个图就是无向图（undirected graph）。如果图里的边只有一个方向，那么这个图就是有向图（directed graph）。你可以将有一个方向和两个方向的边分别当做单行道和双行道。

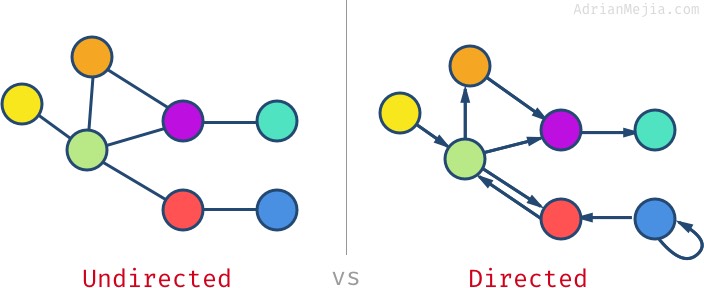
另外，一个顶点还可以拥有通向自己的边，如上图中的蓝色顶点，这被称作自环（self-loop）。

一个图可以有环（cycle），这意味着如果遍历节点，你可能会多次访问同一节点。没有环的图被无环图（acyclic graph）。

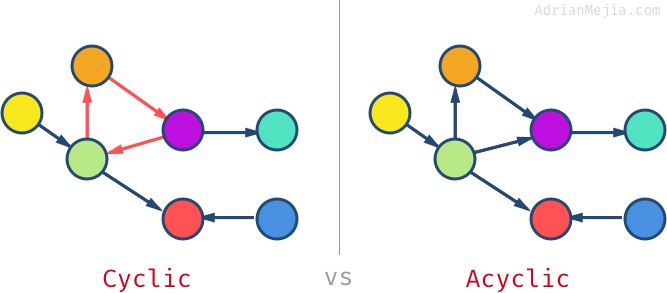
此外，无向无环图也被称作树（tree）。我们将会在下一篇文章中深入介绍树这种数据结构。

在一个图中，并不是所有顶点都必须被连接，你可能会在图里看见孤立的节点甚至分离的子图。如果图里所有的节点都至少有一条边，那么这个图就是一个连通图（connected graph）。当每一个节点都连接到了其他所有节点时，那么我们就有了一个完全图（complete graph）。

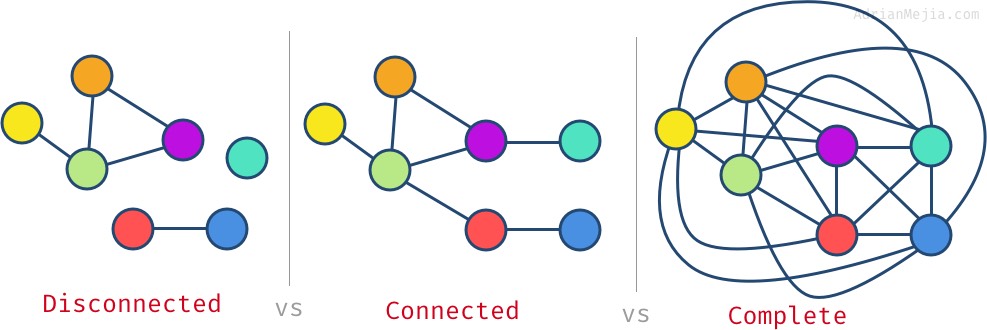
对于完全图来说，每一个节点都有（节点数 - 1）条边。在上面的完全图里，我们有 7 个节点，因此每个节点都有 6 条边。

图的应用

当每条边都具有分配给它们的值或成本（权值）时，我们就说我们有了一个带权图（weighted graph）。如果一个图没有权值，我们可以假定它为 1。下面是一张飞机飞行路线的带权图。

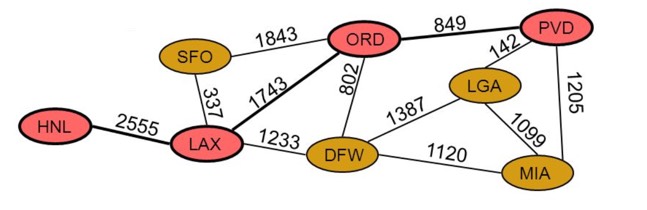
带权图有很多应用方式，这取决于你需要解决什么问题。对于上面的飞行路线图来说，节点代表着机场，边代表着两个机场之间的直飞航班，权值代表着两个机场之间的里程。利用这个带权图和一些图相关的算法，我们可以解决一些实际问题，比如计算出最优的飞行路线。

实际上在现实世界中，图还有很多其它方面的应用。不过在这里我们只介绍基本的图以及它的应用，现在让我们开始学习如何用代码来表示图。

图的表示

我们有两种主要的方式来表示图：

领接表
邻接矩阵

让我们用下面的有向图来作为示例来讲解。

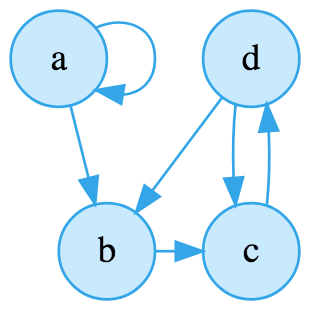
邻接矩阵

所谓的邻接矩阵就是一种使用二维数组（NxN 的矩阵）来表示图的方式。我们首先给每个节点一个索引值，如果两个节点是相连的，那么我们就在代表它们的行列交汇处加 1。如果它们不相连，那么我们就在他它们的行列交汇处加 0 或者填上字符 -。如下所示：

邻接矩阵

  a b c d e
a 1 1 - - -
b - - 1 - -
c - - - 1 -
d - 1 1 - -

如上所示，矩阵在每行每列都列出了所有的节点。如果矩阵中的连接数（即 1 的数量）比较少，那么我们称这个图的稀疏图（sparse graph）。相反地，如果连接的数量比较多，我们就称之为稠密图（dense graph）。如果矩阵被 1 填满了，那么这个图就是一个完全图（complete graph）。

值得注意的是，对于无向图来说，邻接矩阵始终都是关于对角线对称的，而对于有向图来说却并非如此（如上面的矩阵）。

查询两个节点在邻接矩阵中是否相连的时间复杂度为 O(1) 。使用邻接矩阵储存图的空间复杂度为 O(n^2)*，其中 *n 为顶点的数量。我们也表示为 *O(|V|^2)*。

由于顶点被储存为 VxV 的矩阵，每次有一个顶点被添加都会导致矩阵被重建为 V+1xV+1 。因此，添加一个顶点的复杂度为 O(|V|^2) 。

在一个邻接矩阵中，为了获取与一个节点相邻的其它节点，我们需要找到节点对应的行，然后依次读取它与其它节点的边。因此，时间复杂度为 O(|V|) 。

如果你用邻接矩阵来表示 Facebook 上面的人际关系网络，你会发现大多数人其实都不知道其它所有人，最多只知道其中的小部分，你的矩阵是个很典型的稀疏矩阵，大部分的空间都被浪费了。这就是为什么在大多数实现中我们会使用邻接表而不是邻接矩阵来表示图。

邻接表

邻接表是一种最常用的表示图的方式。在使用邻接表来表示图时，每个节点都有一个储存着与它自己相连的节点的列表。

可以使用包含着节点的 Array（或 HashMap）来将图表示为邻接表。每个节点都包含了一个列表（如数组、链表、集合等），这个列表列出了所有与之相连的节点。

拿上面给出的图来说，我们知道 a 有着到 b 和它自己的连接，b 有着到 c 的连接，于是邻接表就会像是下面这个样子：

邻接表

a -> { a b }
b -> { c }
c -> { d }
d -> { b c }

查询在邻接表中节点 a 与节点 b 是否相连时，你需要遍历节点 a 的列表，时间复杂度为 O(n) ，其中 n 为顶点的数量。我们也表示为 O(|V|) 。

将图表示为邻接表的空间复杂度为 O(n) ，其中 n 为顶点和边的数量之和。我们也表示为 O(|V| + |E|) 。

邻接表的 HashMap 实现

邻接表是最常用的表示图的方式，我们有好几种方式来实现邻接表，其中最简单的一种就是使用 HashMap。将节点的值作为 key，将节点的邻接节点列表作为 value。

const graph = {
  a: ['a', 'b'],
  b: ['c'],
  c: ['d'],
  d: ['b', 'c']
}

图通常需要下面的操作：

添加或删除一个顶点
添加或删除一条边

其中添加或删除一个顶点还涉及了邻接列表的更新。

假设我们想要删除顶点 b，我们需要 delete graph['b']; ，但同时我们还需要删除 a 和 d 邻接数组中的 b 元素。

于是每次我们删除一个节点时，我们都必须遍历所有节点的邻接数组，时间复杂度为 O(|V| + |E|) 。有更好的方式吗？我们会在后面解决这个问题。首先还是让我们以更加面向对象（object-oriented）的方式实现我们的邻接表。

邻接表的 OO 实现

让我们先从 Node 这个类开始，它保存了顶点的值以及它的邻接顶点。我们还可以使用辅助函数来添加和删除列表中的相邻节点。

class Node {
  constructor(value) {
    this.value = value;
    this.adjacents = []; // adjacency list
  }

  addAdjacent(node) {
    this.adjacents.push(node);
  }

  removeAdjacent(node) {
    const index = this.adjacents.indexOf(node);
    if(index > -1) {
      this.adjacents.splice(index, 1);
      return node;
    }
  }

  getAdjacents() {
    return this.adjacents;
  }

  isAdjacent(node) {
    return this.adjacents.indexOf(node) > -1;
  }
}

值得注意的是，上面的 adjacents 我们使用的是数组，这会导致 removeAdjacent 的时间复杂度变成 O(|E|) 。更好的方式是使用 HashSet，这样移除操作的时间复杂度可以变成 O(1) 。不过还是让我们先这么实现，后续在对它进行优化。

好的，现在我们已经有了 Node 这个类了，我们还需要一个 Graph 类，这个类将会帮助我们添加/删除顶点和边。

// Graph.constructor
class Graph {
  constructor(edgeDirection = Graph.DIRECTED) {
    this.nodes = new Map();
    this.edgeDirection = edgeDirection;
  }
  // ...
}

Graph.DIRECTED = Symbol('directed graph'); // 有向图
Graph.UNDIRECTED = Symbol('undirected graph'); // 无向图

我们需要知道的第一件事就是我们的图究竟是有向图还是无向图，这会影响我们在添加边的时候的操作。

然后我们需要实现在两个节点之间添加边的操作。我们将一个节点作为源节点，一个节点作为目标节点，以此来指明边的方向。需要注意的时候，如果我们的图是无向图，那么我们还需要添加一条从目标节点指向源节点的边。

addEdge(source, destination) {
  // 先创建顶点
  const sourceNode = this.addVertex(source);
  const destinationNode = this.addVertex(destination);
    
  sourceNode.addAdjacent(destinationNode);
    
  if(this.edgeDirection === Graph.UNDIRECTED) {
    destinationNode.addAdjacent(sourceNode);
  }
    
  return [sourceNode, destinationNode];
}

如果我们想要添加边的两个顶点还不在图中，我们就需要先把它们加入到图中。我们将在下面实现 addVertex 这个方法。

我们添加顶点的方式很简单，把节点加入到 this.nodes 这个 Map 中即可。这个 Map 储存着键值对，key 是顶点的值，value 是 Node 这个类的实例对象，即节点本身。

addVertex(value) {
  if(this.nodes.has(value)) {
    return this.nodes.get(value);
  } else {
    const vertex = new Node(value);
    this.nodes.set(value, vertex);
    return vertex;
  }
}

从图里面删除一个节点需要一点点额外的操作，我们需要检查这个节点是否存在，并且判断它是否作为其它节点的邻接节点而被使用。

removeVertex(value) {
  const current = this.nodes.get(value);
  if(current) {
    for (const node of this.nodes.values()) {
      node.removeAdjacent(current);
    }
  }
  return this.nodes.delete(value);
}

注意，我们这里遍历了每个节点以及它们的邻接表，时间复杂度为 O(|V| + |E|) 。

最后我们需要实现的方法就是删除边的方法了，它和 addEdge 有点相似：

removeEdge(source, destination) {
  const sourceNode = this.nodes.get(source);
  const destinationNode = this.nodes.get(destination);

  if(sourceNode && destinationNode) {
    sourceNode.removeAdjacent(destinationNode);

    if(this.edgeDirection === Graph.UNDIRECTED) {
      destinationNode.removeAdjacent(sourceNode);
    }
  }

  return [sourceNode, destinationNode];
}

这个方法在删除边时首先判断了顶点是否存在，只有都存在时才利用 Node 自带的 removeAdjacent 来删除边。如前面所说，由于 adjacents 使用了数组，这里删除边的时间复杂度为 O(|E|) 。

为了让效率更高，我们接下来将探索如何从节点中搜索值。

广度优先搜索（BFS）

使用广度优先搜索算法遍历图的时候，我们会从初始节点开始依次访问所有节点的邻接表。

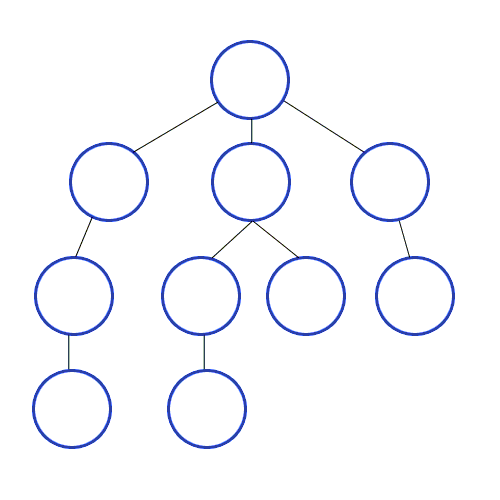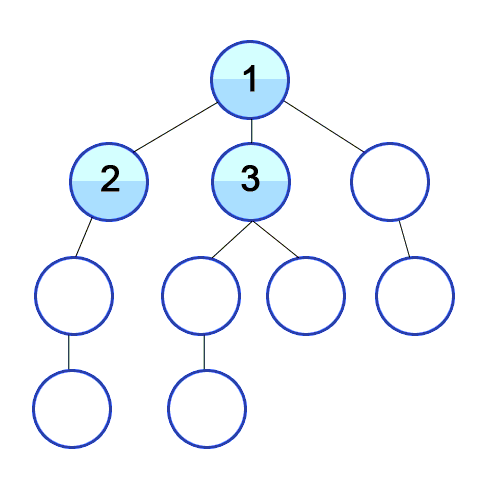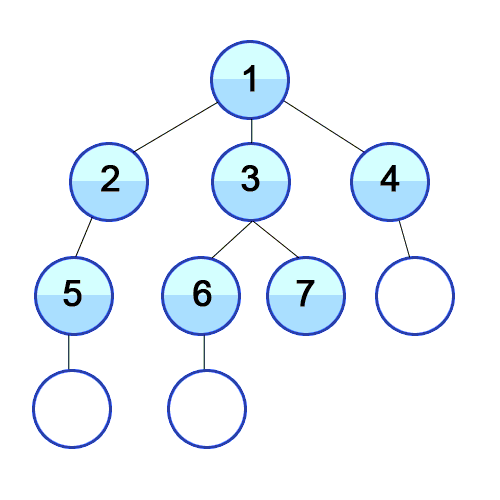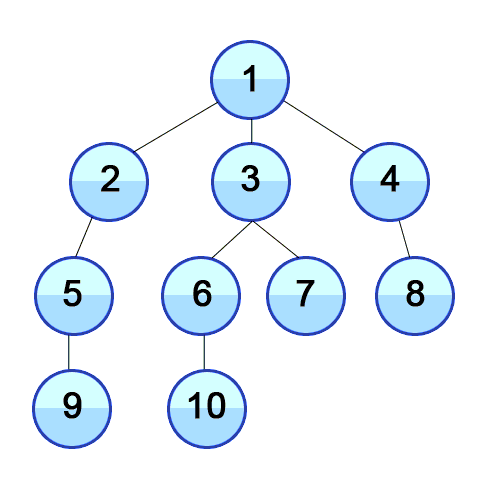
让我们看看如何用代码实现它。

*bfs(first) {
  const visited = new Map(); // 已经被访问过的节点
  const visitList = new Queue(); // 需要被访问的节点

  visitList.add(first); // 第一个被访问的节点

  while(!visitList.isEmpty()) {
    const node = visitList.remove();
    if(node && !visited.has(node)) {
      yield node;
      visited.set(node);
      node.getAdjacents().forEach(adj => visitList.add(adj));
    }
  }
}

正如你所看到的，我们在代码中使用了 Queue 这个队列，它包含了需要被访问的节点。first 节点是第一个需要被访问的节点，它最先入队，也最先出队（FIFO）。

我们也使用了 JavaScript 的 Generator 函数，注意 bsf 函数前面的那个 * 号（Generator 函数的用法可以参见 ECMAScript 6 入门）。我们使用 Generator 函数一次只访问一个元素，这在图的节点数特别多的时候很有用，因为大多数情况下我们没有必要一次性访问所有的节点。

下面是一个如何使用 BFS 的示例：

const graph = new Graph(Graph.UNDIRECTED);
const [first] = graph.addEdge(1, 2);

graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(5, 2);
graph.addEdge(6, 3);
graph.addEdge(7, 3);
graph.addEdge(8, 4);
graph.addEdge(9, 5);
graph.addEdge(10, 6);

bfsFromFirst = graph.bfs(first);
bfsFromFirst.next().value.value; // 1
bfsFromFirst.next().value.value; // 2
bfsFromFirst.next().value.value; // 3
bfsFromFirst.next().value.value; // 4
// ...

你能在这里找到更多的测试用例。接下来让我们看看 DFS 算法。

深度优先搜索（DFS）

深度优先搜索算法是另一种遍历图的算法，我们会从初始节点开始，递归地访问当前节点的第一个相邻节点。

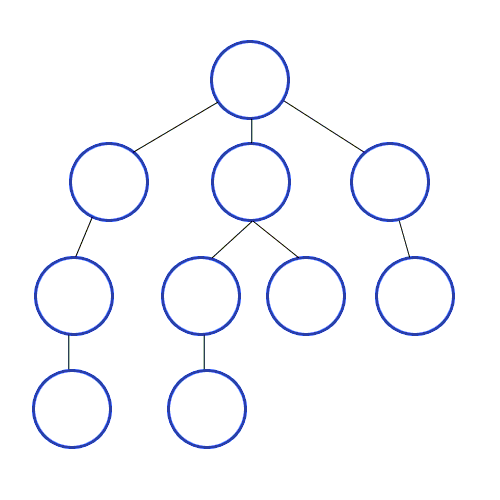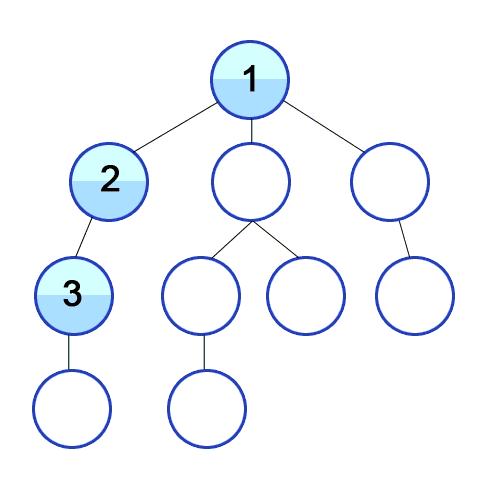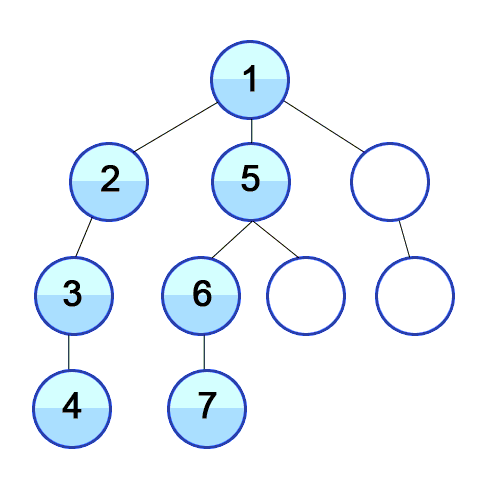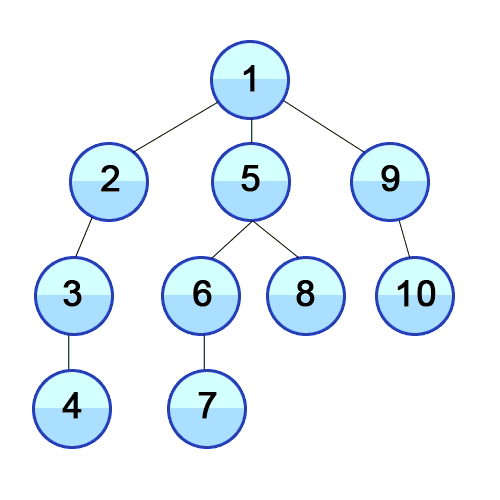
DFS 的迭代实现与 BFS 相同，但不是使用 Queue 而是使用 Stack：

*dfs(first) {
  const visited = new Map(); // 已经被访问过的节点
  const visitList = new Stack(); // 需要被访问的节点

  visitList.add(first); // 第一个被访问的节点

  while(!visitList.isEmpty()) {
    const node = visitList.remove();
    if(node && !visited.has(node)) {
      yield node;
      visited.set(node);
      node.getAdjacents().forEach(adj => visitList.add(adj));
    }
  }
}

下面是一个使用示例：

const graph = new Graph(Graph.UNDIRECTED);
const [first] = graph.addEdge(1, 2);

graph.addEdge(1, 3);
graph.addEdge(1, 4);
graph.addEdge(5, 2);
graph.addEdge(6, 3);
graph.addEdge(7, 3);
graph.addEdge(8, 4);
graph.addEdge(9, 5);
graph.addEdge(10, 6);

dfsFromFirst = graph.dfs(first);
visitedOrder = Array.from(dfsFromFirst);
const values = visitedOrder.map(node => node.value);
console.log(values); // [1, 4, 8, 3, 7, 6, 10, 2, 5, 9]

正如你所看到的，虽然 BFS 和 DFS 使用的图是一样的，但它们的节点遍历顺序却是完全不同的。BFS 是按顺序访问 1 ~ 10，而 DFS 则是在每个节点上尽可能的深入。

时间和空间复杂度

在上面的内容中我们已经实现了 Graph 的基本操作了，比如如何添加和删除边和顶点。下面是一份复杂度的摘要：

	Adjacency List	Adjacency Matrix
Space	O(V + E)	O(V^2)
addVertex	O(1)	O(V^2)
removeVertex	O(V + E)	O(V^2)
addEdge	O(1)	O(1)
removeEdge (using Array)	O(E)	O(1)
removeEdge (using HashSet)	O(1)	O(1)
getAdjacents	O(E)	O(V)
isAdjacent (using Array)	O(E)	O(1)
isAdjacent (using HashSet)	O(1)	O(1)

可以看到在使用了 HashSet 之后的各项操作的效率都是很不错的。

总结

在上面的内容中我们实现了关于图的一些基本数据结构和算法，相信你对图已经有所了解了。不过令人遗憾的是，原作者似乎没有讲解求最短路径的算法，有关这个读者就自行学习吧。